دایره
خوب قراره راجب دایره صحبت کنیم
.
دایره رو با شعاع و مرکزش مشخص میکنیم و بدیهی است که دو دایره با شعاع یکسان هم نهشت هستند و همه دایره ها با هم دیگه متشابه هستند
در علم هندسه ما دایره رو اینجوری نمایش میدیم
C(O,R)
او که به معنی مرکز دایره هست و آر هم به معنای شعاع دایره
وضعیت دایره و نقطه
خوب حالا بریم سراغ وضعیت های مختلف نقطه و دایره
نقطه در دایره سه وضعیت داره
- داخل دایره
- روی دایره
- خارج دایره
اینم تصاویرشون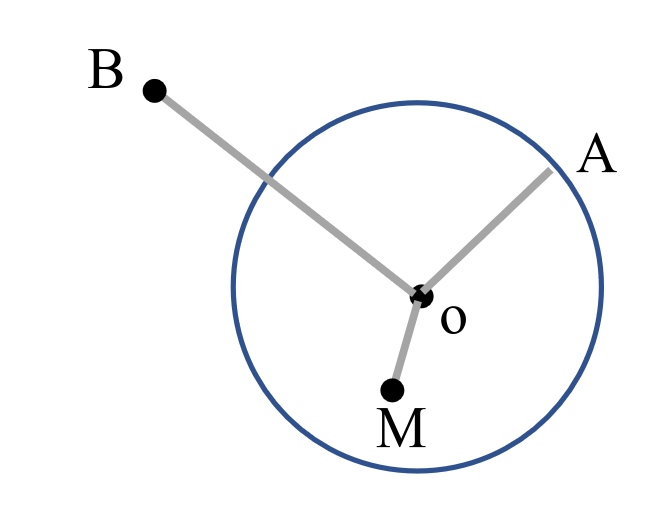
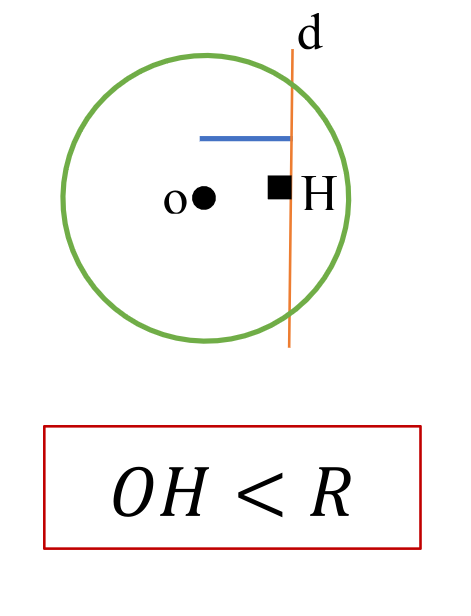
به دیگر سخن اگر فاصله اون نقطه از مرکز کمتر از شعاع باشه اون نقطه داخل دایره و اگر برابر شعاع باشه روی دایره و اگر بیشتر از شعاع باشه خارج دایره قرار داره
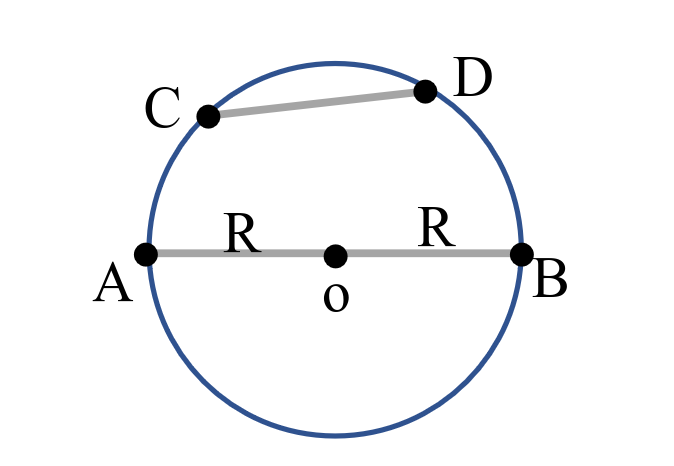
وتر
خوب حالا قراره راجب وتر ها صحبت کنیم وقتی دو تا نقطه متمایز روی دایره رو به هم وصل میکنیم میشه وتر و وقتی مرکز دایره در امتداد اون دو نقطه قرار میگیره اون وتر میشه قطر که فاصله اون برابر است با
2R
وضعیت خط و دایره
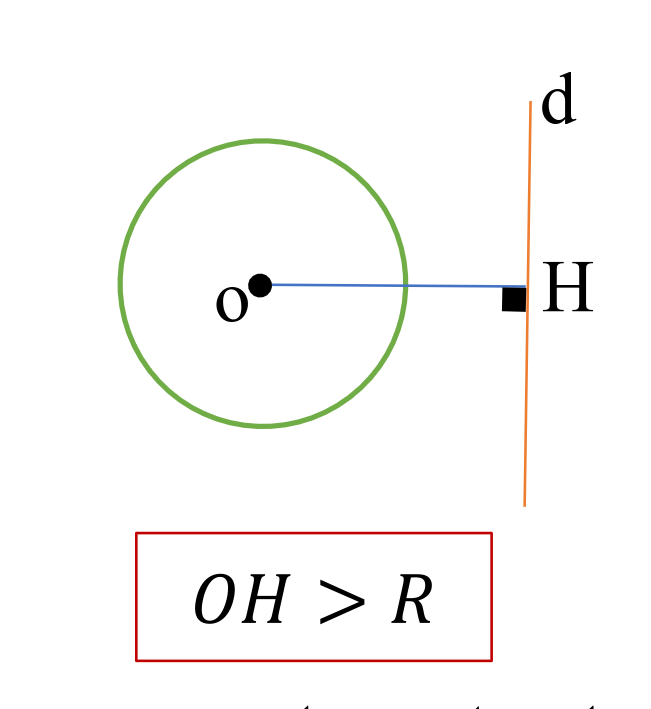
خوب اینم از این بریم سراغ وضعیت خط و دایره
خط و دایره متخارج
- خط دایره متخارج
خط و دایره مماس
- خط و دایره مماس
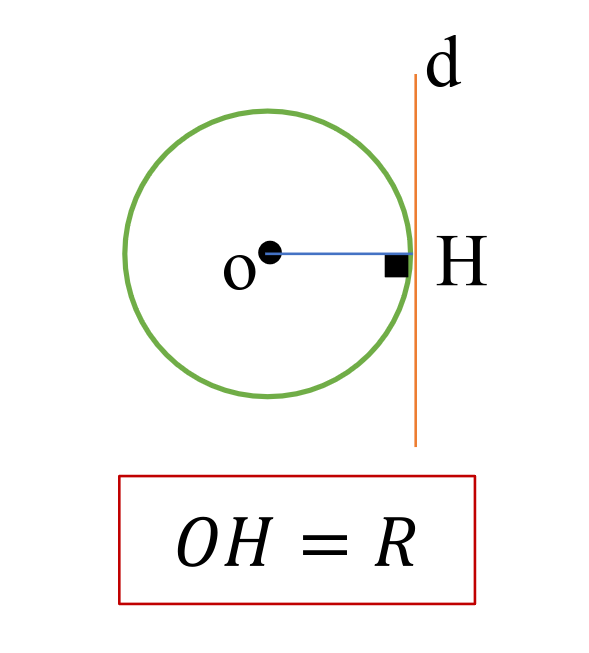
در یک صفحه، خط و دایره بر هم مماساند اگر و تنها اگر این خط بر شعاع در نقطه ی تماس عمود باشد.
خط و دایره متقاطع
- خط و دایره متقاطع
انواع زاویه در دایره
خوب بریم سراغ انواع زاویه در دایره
- مرکزی
- محاطی
- ظلی
- خارجی
- داخلی
زاویه مرکزی
خوب زاویه مرکزی که خیلی راحته یعنی درواقع همشون راحتن ولی اینکه از کدوم توی سوال ها استفاده کنی و سوال رو حل کنی سخته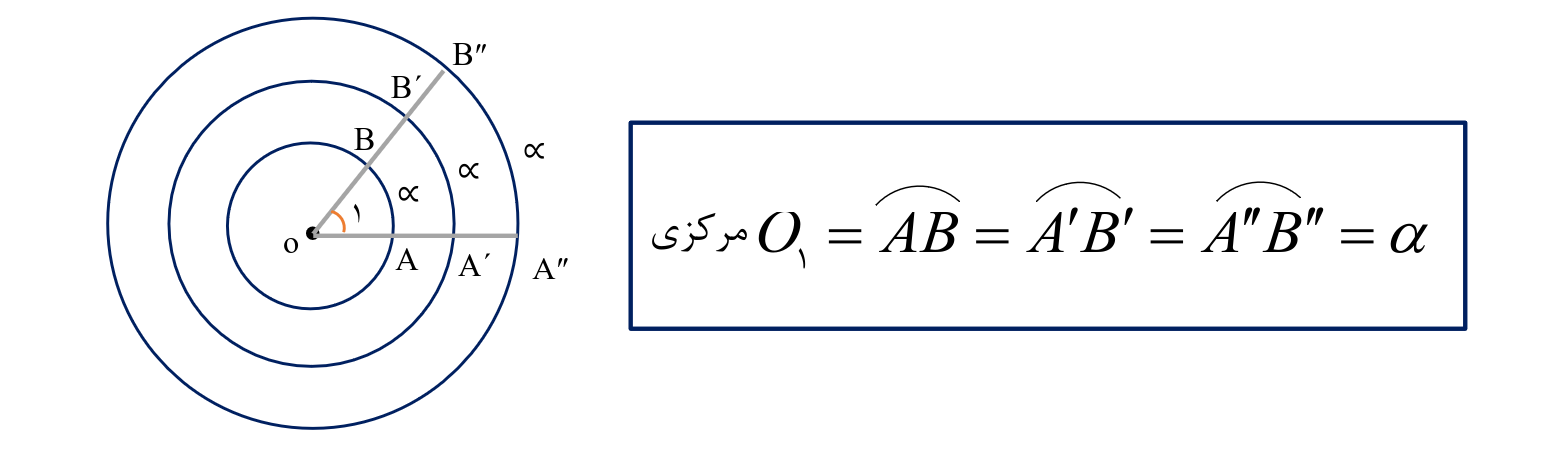
طول کمان
حالا فرض کن میخوای طول کمان رو پیدا کنی راحت با یک جدول تناسب میشه حلش کرد
| 60(یا هر زاویه) | x |
|---|---|
| 360 | 2πR |
مساحت کمان
با جدول تناسب بالا طول هر کمان یا حالا میتونید تغییرش بدید و مساحت یک اسلایس از یک دایره رو به دست بیارید
| 60(یا هر زاویه) | x |
|---|---|
| 360 | πR**2 |
زوایه محاطی
خوب زاویه محاطی که نصف کمان رو به روش هست و بادی خیلی حواست باشه چون گاهی اوقات نمیبینیشون
این فرمول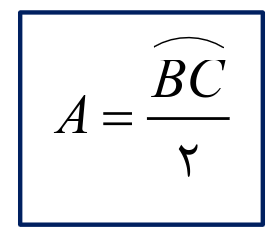
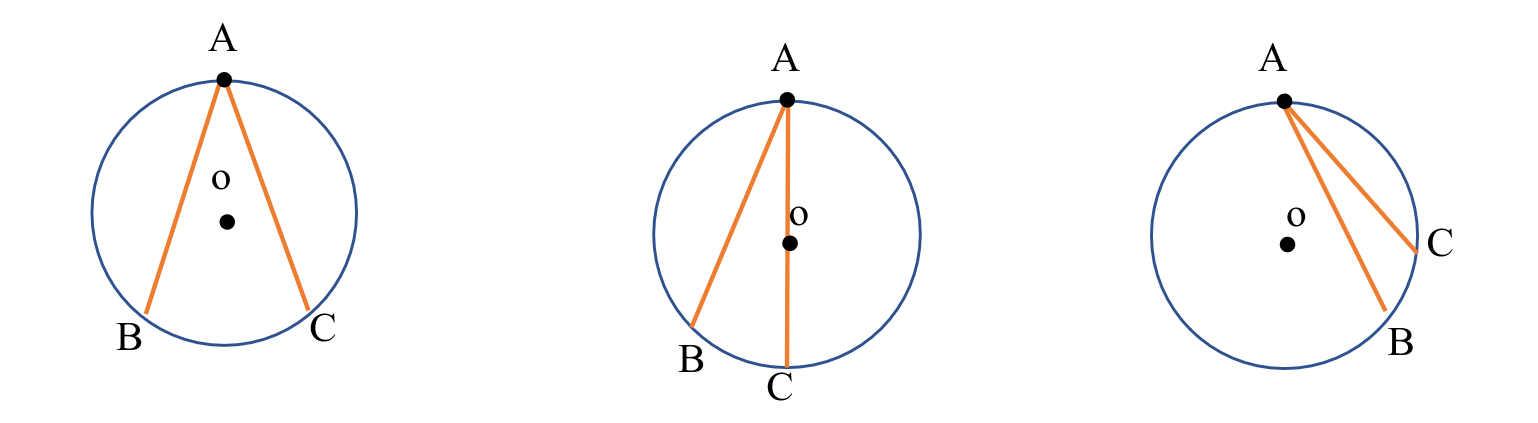
اینم مثال هاش که حالا هر کدوم اثبات خاص و جداگانه ای داره
که بهش نمیپردازیم
زاویه ظلی
خوب زاویه طلی که راحته و یک نکته مهم داره
این فرمولش
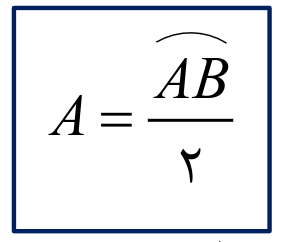
و اینم مثال هاش دقت کنید چه کمانی تقسیم بر دو میشه
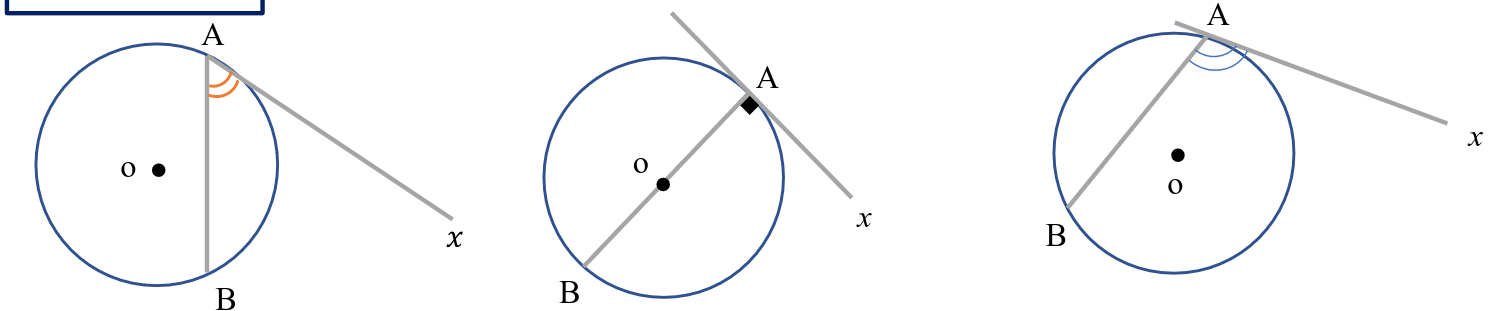
و حالا نکته مهم اینه که
اون دو تا زاویه یک با هم برابرند
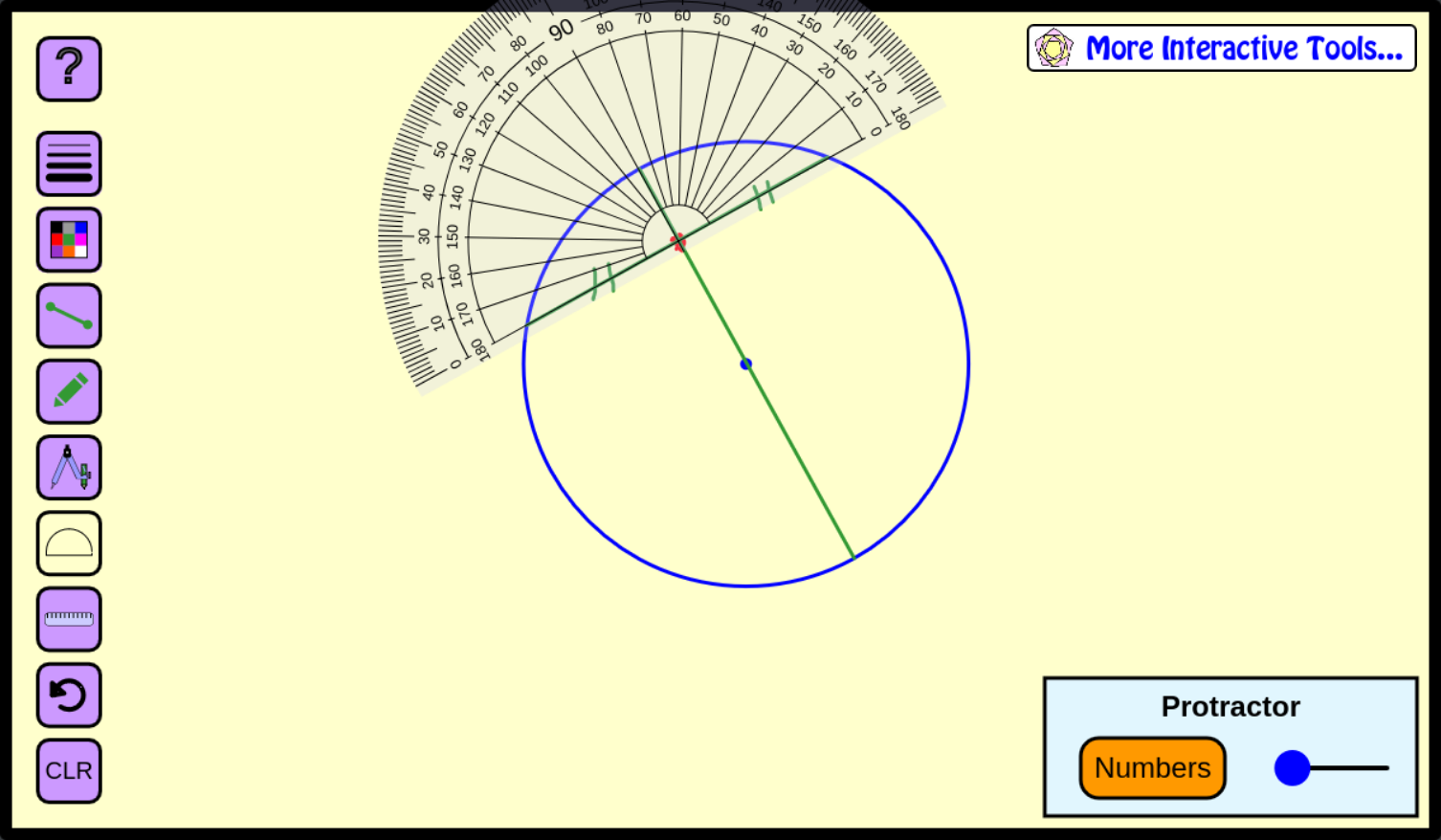
شکل بالا رو هم با ابزار زیر کشیدم
tool
وتر و کمان
خب الان چند تا قضیه داریم که باید بگیمشون چیزی حاصی نیست
در دایره کمان های مساوی برابر و وتر های نظر های نیز برابر است و برعکس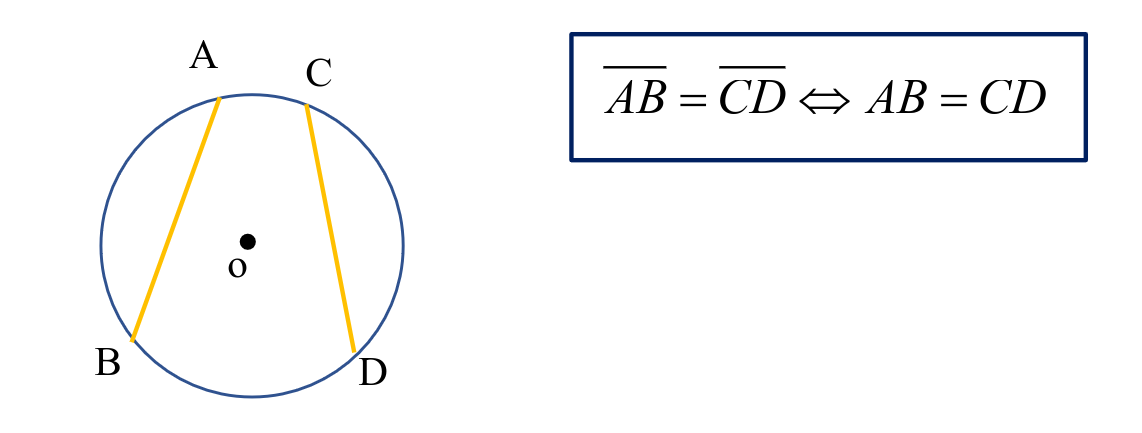
کمان های محصور در دو خط موازی
کمان های محصور در دو خط موازی با هم برابر هستند اما عکس آن همیشه برقرار نیست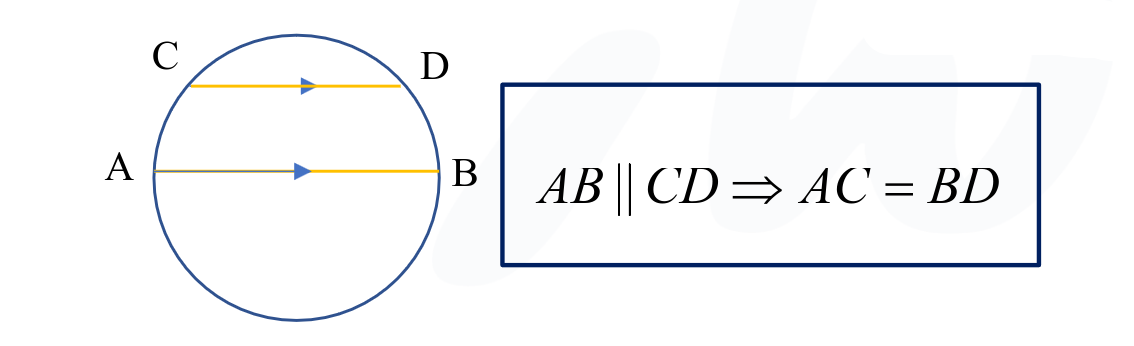
عمود کردن قطر بر وتر و قضایای آن
در دایره قطر عمود بر وتر وتر و کمان ها نظیر آن را نصف میکند
خطی که از مرکز دایره تا وسط وتری را به هم وصل میکند بر آن وتر عمود است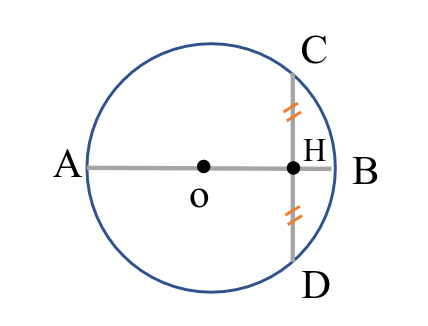
قطری که از وسط یک کمان بگذرد بر وتر نظیر آن عمود است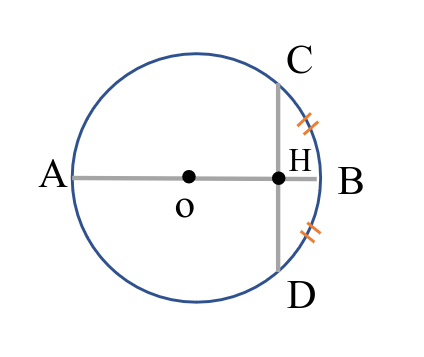
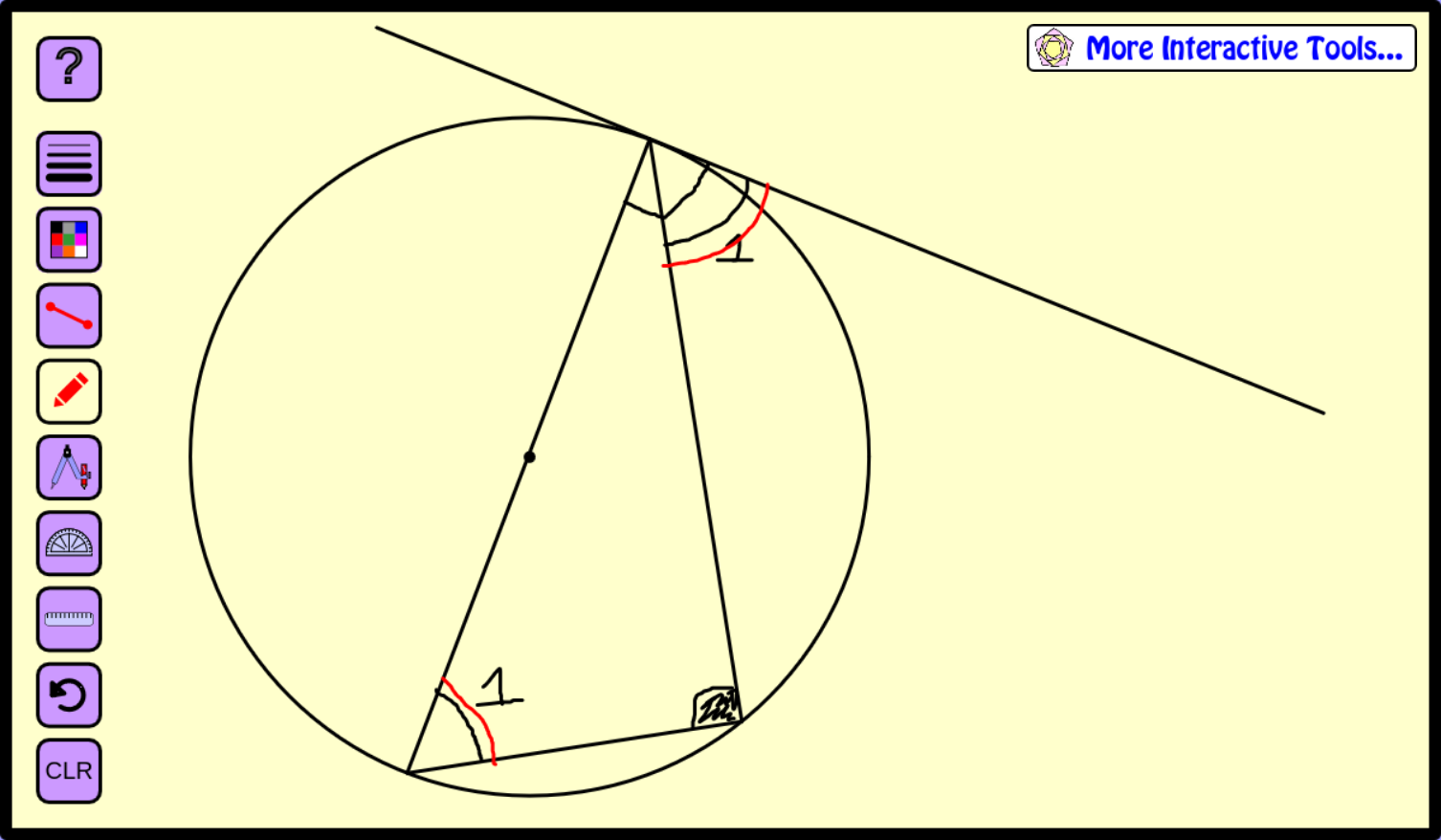
زاویه خارجی
خوب دیگه دهنم صاف شد بسه بریم سراغ زاویه خارجی
که سه تا حالت متفاوت داره اما با یک فرمول حل میشن و این خداییش خوبه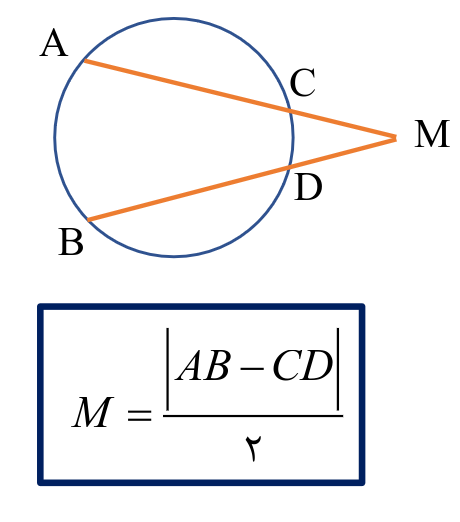
خوب تو بالایی که سر راست اصولا به این فرمول میگن کم دوم تفاوت کمان ها رو به دست میاری و بعدش تقسیم به دو میکنی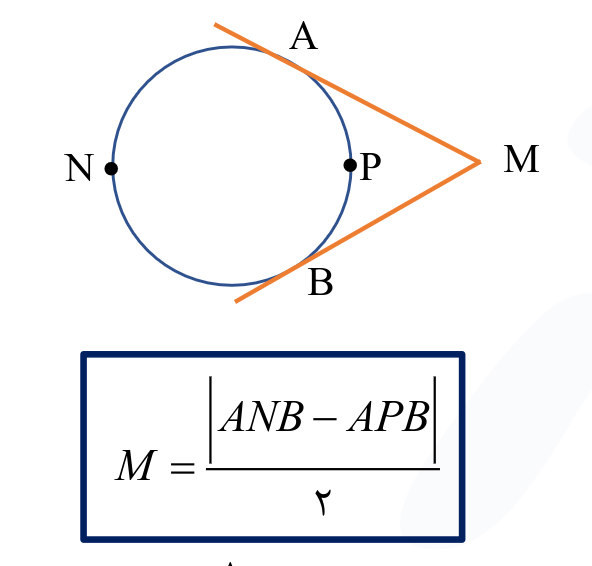
اینجا هم که خط ها مماس شدن فرقی نمیکنه بازم با همون فرمول و کانسپت حل میشن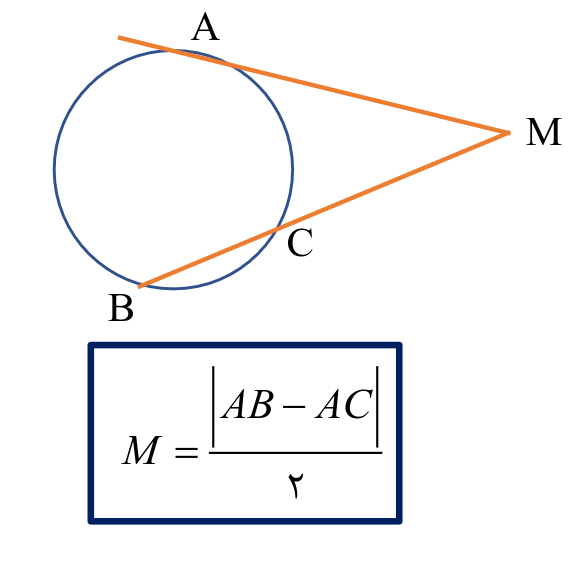
درباره اون قدر مطلق ها هم باید بگم که چون ممکنه جواب منفی بشه و اختلاف داریم میزاری
زاویه داخلی
خب بریم سراغ زاویه داخلی که اصولا بهش میگن جمع دوم دفعه پیش کم میکردیم و تقسیم به دو میکردیم الان جمع میکنیم و تقسیم به دو میکنیم
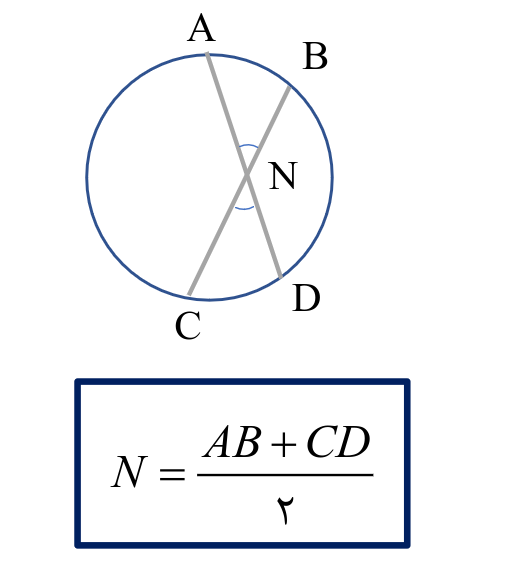
کوچکترین و بزرگترین وتر گذرنده از یک نقطه داخل دایره
خوب و برای پایان دادن به بخش صفر میخوام با مثلث قائم و الزاویه گیجتون کنم
فقط قبلش یک جمله جالب بگم هر چه وتر بزگتر باشد به مرکز نزدیک تر است و برعکس
یعنی اگر وتر کوچیک باشه فاصله بیشتری از مرکز داره
از یک نقطه داخل دایره هزاران وتر میگذره و بزرگترینش قطر دایره هست و برای به دست اوردن کوچیک ترینش باید وتری رسم کنیم که به قطر دایره ای که در امتداد اون نقطه هست عمود باشه بزارید با شکل بگم درکش سخته
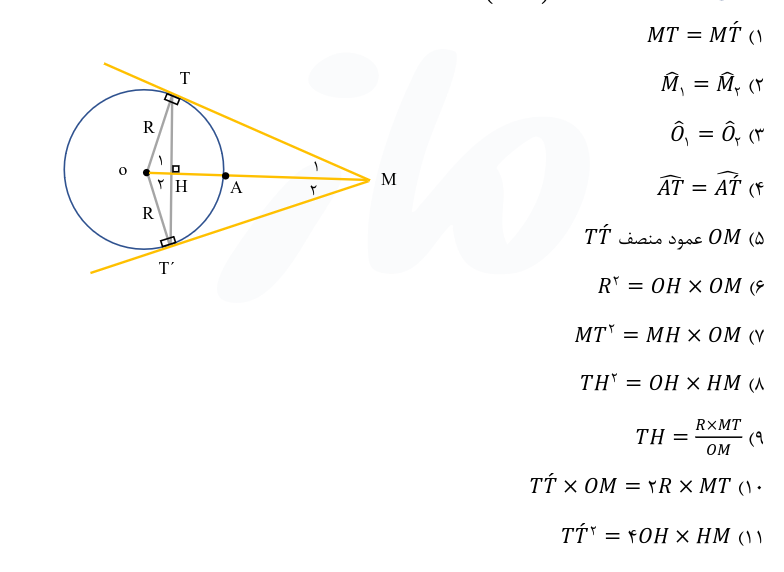
روابط طولی مثلث قائم و الزاویه در دایره و نقطه ای خارج از آن
خوب بریم سراغ روابط مثلث قائم و الزاویه کلی رابطه هست و توضیح دادنشون طولانی عکس رو میزارم خودتون میتونید مطالعه اگر روابط مثلث قائم و الزوایه رو بلدید
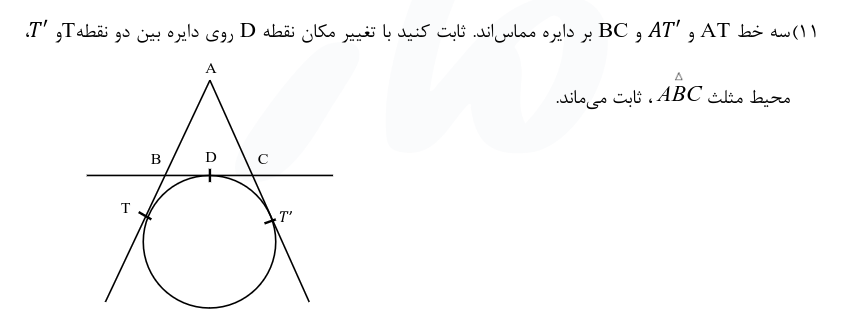
حل یک سوال اثباتی
خوب در بخش پایانی میخوام یک سوال خیل خفن هم حل کنم که اینو روی کاغذ میزارم
متن سوال:
حل سوال :
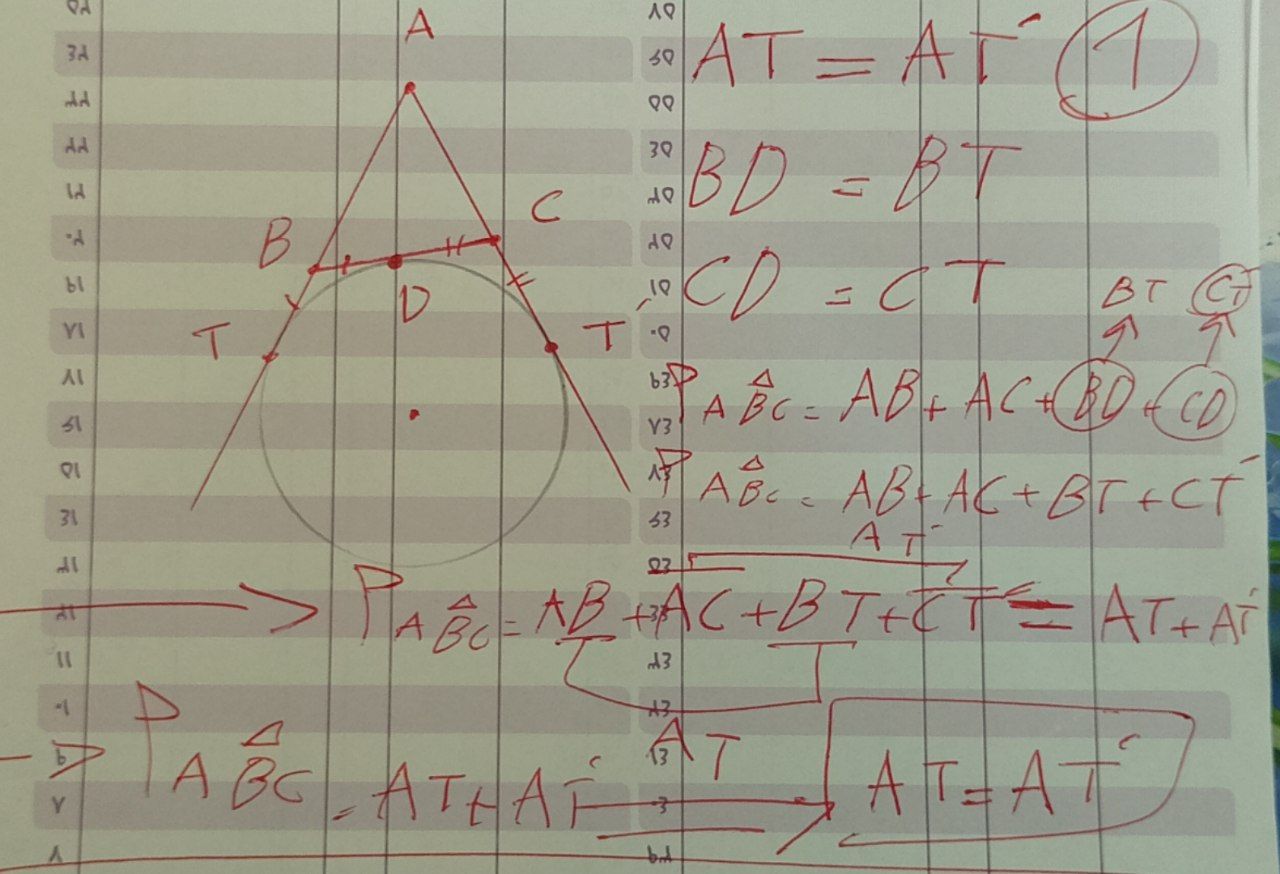
خب اینم از داستان زاویه ها توی بلاگ بعدی میریم سراغ روابط طولی در دایره که جلو جلو پستش رو میزارم